Llamamos sección cónica (o simplemente cónica) a cualquiera de las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.
En la siguiente imagen observamos la parábola (1), elipse y circunferencia (2), hipérbola (3)
 |
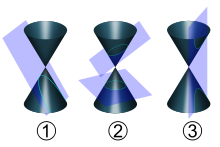| Crédito al AUTOR: De Pbroks13 - Trabajo propio, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=5919064 |
Apolonio de Perga (Nació alrededor del 262 a. C. en Perga, Grecia Ionia (Ahora Turquía) y falleció: Alrededor del 190 A.C en Alejandría, Egipto). Fué el primer matemático que inició el estudio de las cónicas (universidades de Alejandría y Pérgamo). Su estudio lo plasmó en su tratado “Cónicas”, que constaba de ocho ibros. Cuatro de ellos se conservan originales, otros tres gracias a la traducción al árabe llevada a cabo por Thabit ibn Qurra, habiendo desaparecido el octavo. En 1710, Edmund Halley, el astrónomo, publicó una traducción de los siete libros conocidos en latín.
Cónicas de Apolonio. Traducción al árabe
 |
| Crédito al AUTOR: De Apollonius of Perga - http://bodley30.bodley.ox.ac.uk:8180/luna/servlet/view/search?q=Title=%22Conica.%20Book%201-7%22, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=40713030 |
APLICACIÓN DE LAS CÓNICAS:
1.- Estudio del movimiento de los planetas, debido a que estos siguen órbitas elípticas, en uno de cuyos focos se encuentra el Sol, característica utilizada por Kepler en su estudio sobre los planetas y por Newton en Ley de Gravitación Universal.
2.- Estudio de los movimientos de los proyectiles, tiro horizontal y parabólico.
3.- Construcción de antenas y radares, sabiendo que cualquier onda que incide sobre una superficie parabólica, se refleja pasando por el foco.
| Crédito al AUTOR: De Drini - Trabajo propio, GFDL, https://commons.wikimedia.org/w/index.php?curid=4675993 |
PLANIFICACIÓN AULA: CIRCUNFERENCIA: 13-02-17
A) Definición
B) Ecuación de la circunferencia con centro en el origen O(0,0) y radio r
C) Ecuación circunferencia con centro en el punto O(a,b) y radio r
D) Ecuación general de la circunferencia
E) Ecuación de la rectas tangentes y normales a la circunferencia
F) Cálculo de la recta normal
G) Cálculo de la recta tangente
H) Posiciones relativas de dos circunferencias
I) Ejercicios prácticos
No hay comentarios:
Publicar un comentario